Task M: Mathematics of Carbon Manifolds
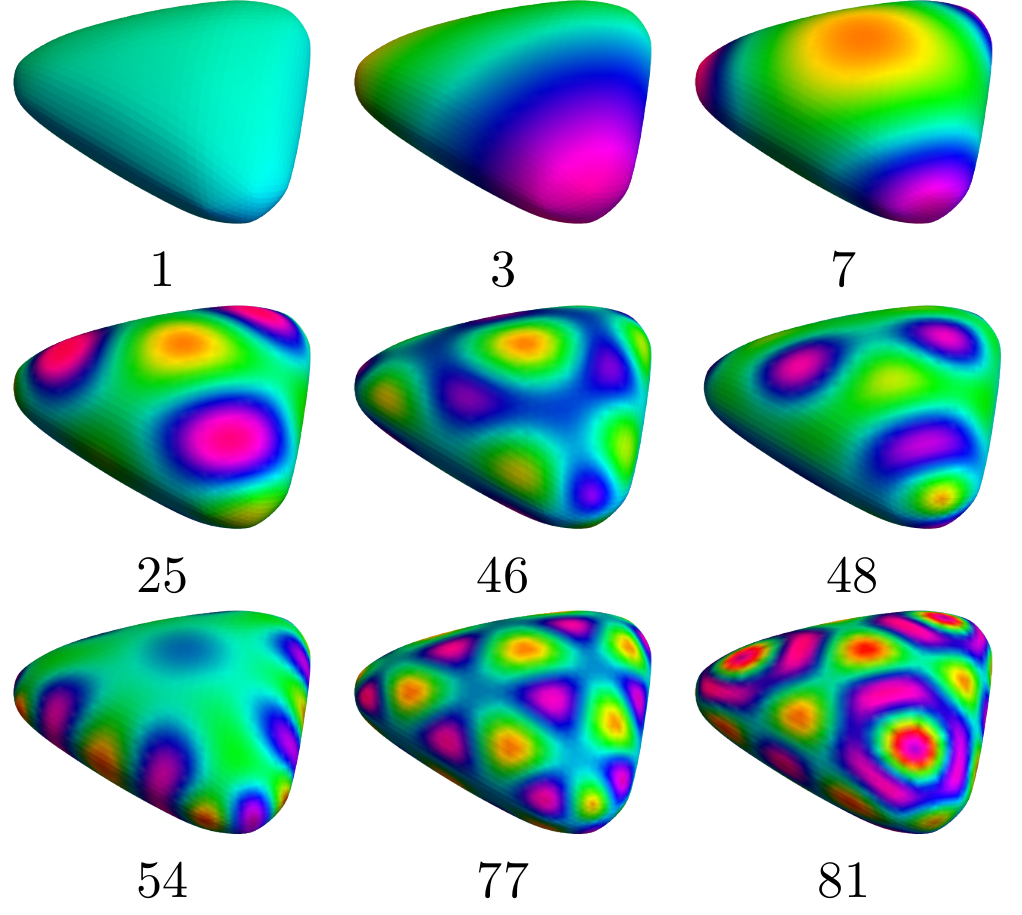
Task W: Wave Equations on Carbon Manifolds
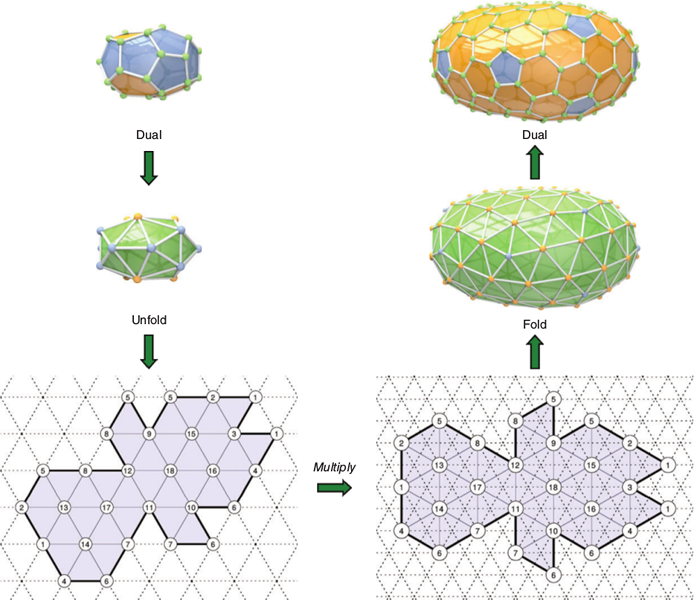
Task E: Isometric Embeddings
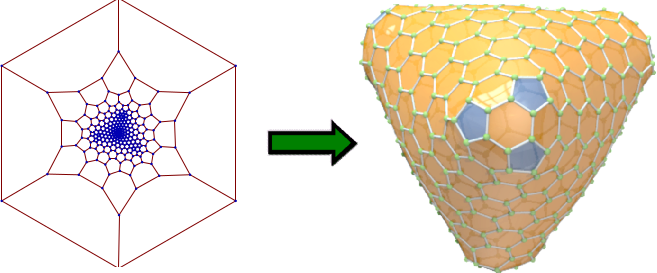
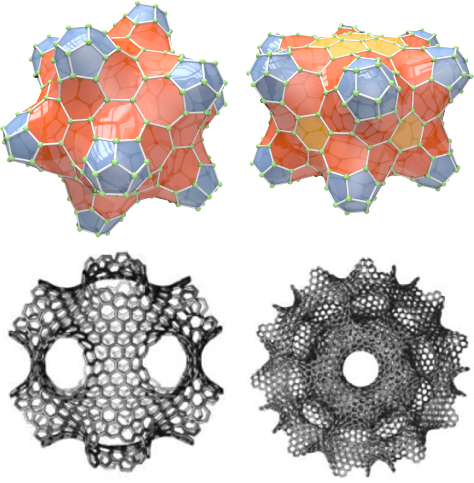
Task F: Fulleroids, Schwarzites, and Beyond
Task P: Approximation of Molecular Properties
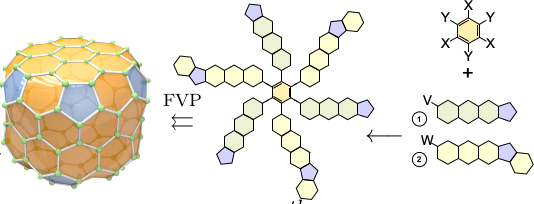
Task R: Paths to Rational Synthesis
Is it possible to calculate the molecular properties of two-dimensional structures through intrinsic surface geometries derived from their bond graphs, side-stepping week-long quantum chemistry geometry optimizations? And can the same formalism be used to find pathways to chemical synthesis of these 2D-materials?
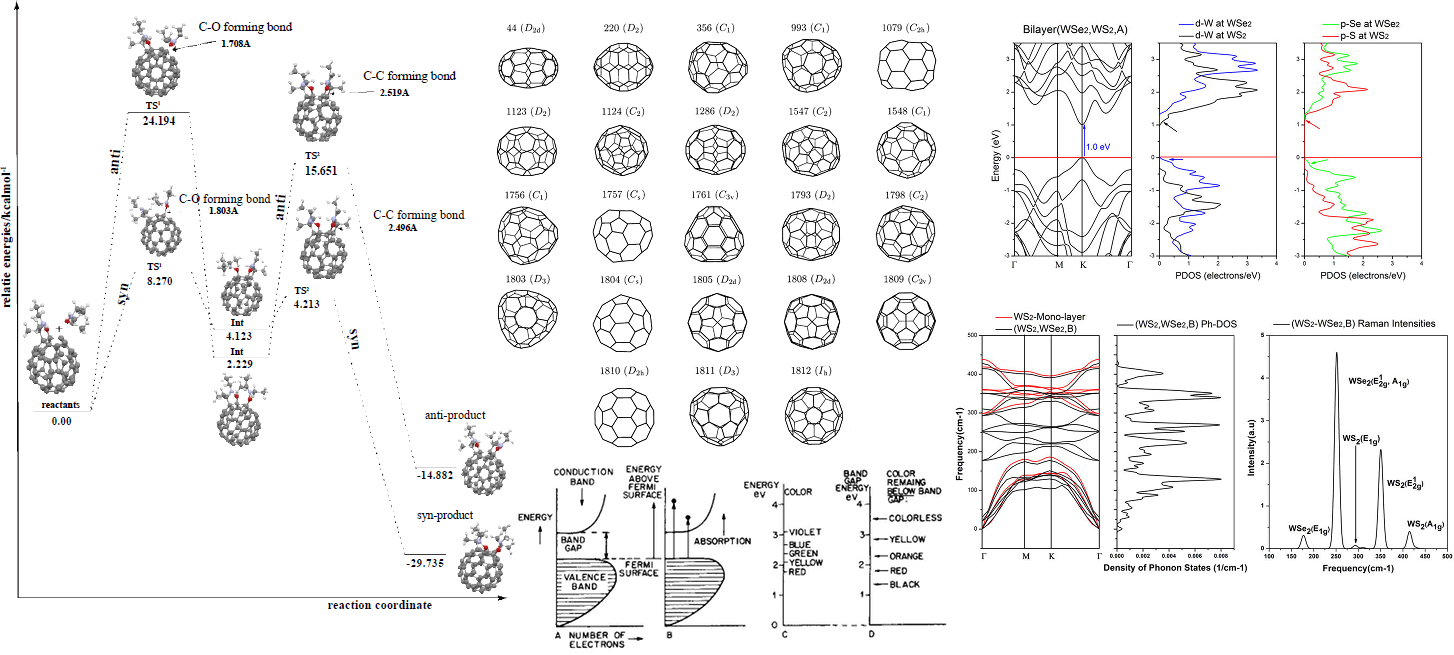
This project investigates how discrete geometry can be used to understand polyhedral molecules, in particular those that can be formed by a single layer of carbon atoms. These are called Fullerenes, and form extraordinarily strong polyhedral cages of many shapes. To date, only a few types have been synthesized, namely the C60 "Buckyball" and nanotubes, but these have already created revolutionary materials with important uses in medicine, solar cells, energy storage, artificial muscles, and more.
The theoretically possible structures abound, for example 132,247,999,328 distinct C400 fullerene molecules can be formed, each with its own chemical and physical properties: a systematic quantum chemical analysis of them all would take millions of years with current methods.
The aim is to develop new mathematical methods, algorithms, and software to analyze fullerenes many orders of magnitude faster than presently possible. The core idea is to solve wave equations directly on non-Euclidean surface geometries, computed from combinatorial geometry in microseconds. With computational methods fast enough to search through the many millions of theoretical structures, we can find the needles in the haystack that can be synthesized, and that have chemical and physical properties of our choosing.
Using the same mathematical tools, we calculate planar molecules that fold up to desired fullerene structures by autoassembly. The goal is algorithmic discovery of recipes for chemical synthesis.
This project introduces new formalisms that form a bridge between chemical graphs methods and full quantum chemistry. This is achieved through geometrical structures, which I have named carbon manifolds, that arise naturally from the mathematics of fullerenes and other graphene-like carbon surfaces. These will be leveraged to devise algorithms and build software enabling the study of electronic wave equations directly on the manifold geometries, radically more efficient than solving full wave equations. The goal is predictive approximation methods millions of times faster than current state of the art ab initio calculations, facilitating systematic screening of entire isomer spaces to identify structures of interest. The same geometric formalism will be leveraged to aid discovery of direct synthesis paths of specific fullerene isomers, a presently unsolved problem. Generalizations are proposed to extend the methods beyond fullerenes to more complex carbon allotropes, as well as low-dimensional structures containing other atoms.
James Avery (avery@nbi.ku.dk)