Research interests in a nutshell
My research encompasses various aspects of solid-Earth geophysics.
To investigate the inaccessible Earth we have to rely on indirect
measurements, therefore we need methods to
estimate the unknown parameters that are able to predict the observations.
My interests concern the development of methodologies and implementation of
algorithms to model these geophysical data, including
processing, forward and inverse modeling.
Research topics include mainly inverse problems in geophysics,
seismology and computational geophysics, and touch other fields like
applied geophysics and geochemistry. I am strongly interested in the
probabilistic approach to inverse problems, in particular in Monte Carlo
methods. These are able to tackle complex non-linear inverse problems
and can combine together different geophysical data sets.
Hamiltonian Monte Carlo inversion and Nullspace Shuttles
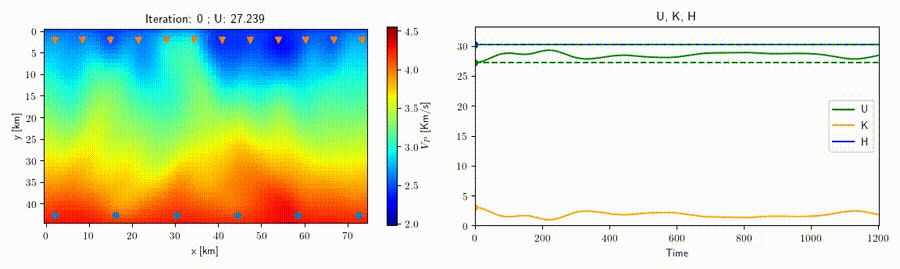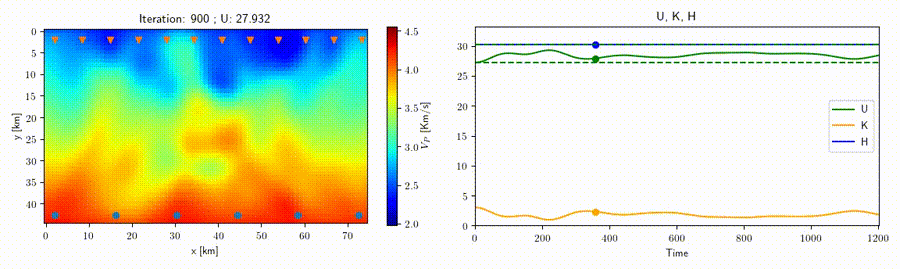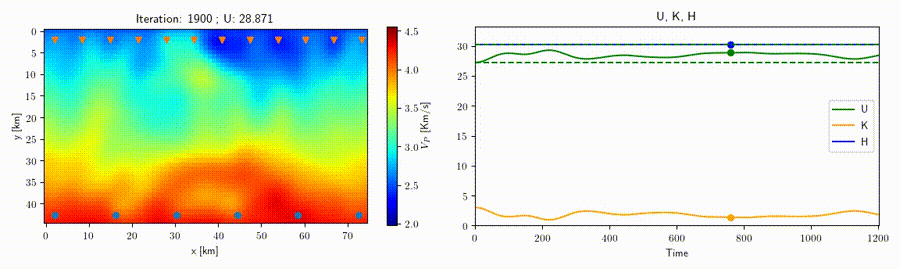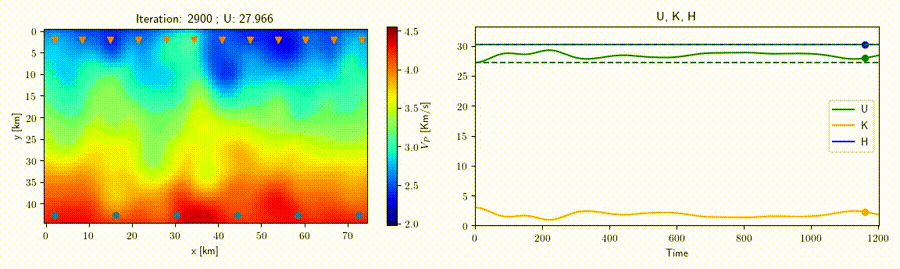
In collaboration with Prof. Andreas Fichtner (ETH Zurich) we study the application of the Hamiltonian Monte Carlo method to geophysical inverse problems such as seismic tomography to help improve sampling techniques for high-dimensional nonlinear problems. This strategy rests on the construction of an artificial Hamiltonian system which allows us to exploit the information provided by the gradient of the misfit function to sample the posterior distribution. A related idea is that of a "nullspace shuttle", an algorithm which is capable of exploring alternative solutions with respect to an optimal model while remaining within a prescribed tolerance from the optimal misfit function value. An example for traveltime seismic tomography is shown in the movie above, where all the varying velocity models shown produce a misfit (green line) within the given tolerance.
Large linear inverse problems
Recently we have developed a methodology to address in an efficient manner large linearizable inverse problems where the uncertainty can be assumed to be Gaussian and the covariance matrices and forward modeling are separable, see https://doi.org/10.1016/j.cageo.2018.09.005.
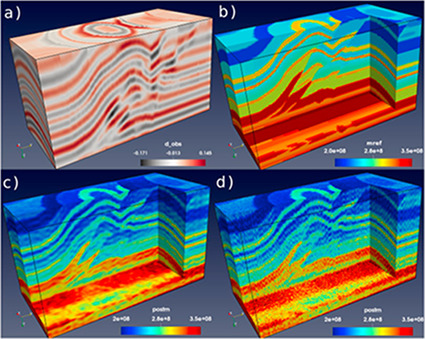
Combined inverse modeling and geostatistics in a probabilistic framework
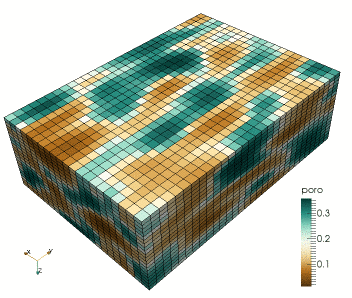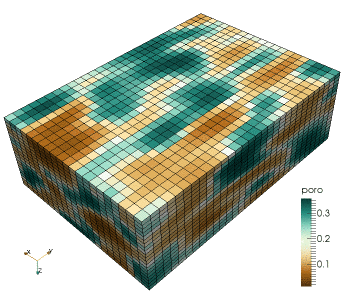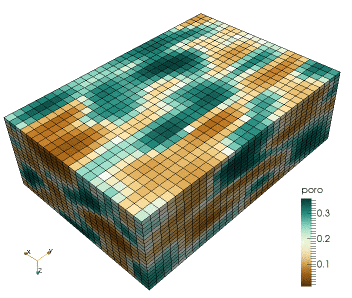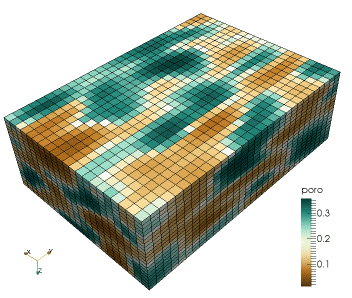
This research regards the study of a combined geophysical and geostatistical inversion method in the framework of a probabilistic approach targeting subsurface structure and related uncertainty analysis (Computational Geophysics group - Prof. K. Mosegaard). This involves the development of Monte Carlo (Markov chain Monte Carlo) methods that samples the posterior distribution of reservoir models according to the degree of fit with observed seismic data and the a priori information. It involves algorithms drawn from geostatistics to generate random models according to possibly complex prior information, e.g., by patterns "learned" by the algorithm by scanning through prototype models provided in the form of training images.
Markov Chain Monte Carlo inverse methods applied to thermo-compositional mapping of Earth's mantle

In collaboration with Dr. Amir Khan (ETH Zurich) we are investigating the thermo-chemical structure of Earth's mantle using a probabilistic methodology to invert seismic and other geophysical data. We employ a non-linear Monte Carlo approach in a bayesian framework that combines a self-consistent thermodynamic modeling of mineral phase equilibria with seismic forward modeling (surface waves dispersion curves or full waveform), targeting directly thermo-compositional mapping of Earth's mantle.
